Questo articolo è il frutto di una ricerca svolta nella Federazione "DAC - Crick & Croack", ricerca gestita da specialdoc, manager di Biotek Team, che l'ha curata per sei mesi. A tutti i confederati DAC che hanno partecipato un grande grande GRAZIE, a specialdoc il merito per tutto lo sbattimento e il ringraziamento per avermi lasciato la parti più divertente, l'elaborazione dei dati.
OverConfidence (abbreviata in "OC"), immagino sappiate già di cosa si tratti, ad ogni modo riprendo dal manuale, considerando anche le precisazioni comunicate nel messaggio del Notiziario del 2 agosto 2010.
Nel caso in cui incontri una squadra piazzata peggio di te e la tua fiducia è forte o maggiore, i tuoi giocatori possono sottovalutare gli avversari e giocare al di sotto delle loro normali possibilità.
Il rischio di sottovalutare l'avversario dipende dalla differenza di punti e di posizione tra le due squadre, dal tuo livello di fiducia e dall'atteggiamento della tua squadra per la partita. Più grande è la differenza tra le squadre, più alta è la fiducia, maggiore è il rischio. Il solo modo per evitare completamente il rischio di sottovalutare l'avversario è quello di giocare "partita della stagione".
Nel caso in cui la tua squadra sottovaluti l'avversario, i punti di differenza, il livello della fiducia, l'atteggiamento della squadra e il fattore campo, sono i fattori che ne determinano l'entità. In base al risultato puoi però recuperare nell'intervallo tra i due tempi: recupero totale se in svantaggio, 2/3 se in pareggio, 1/3 se in vantaggio di un gol.
OverConfidence (abbreviata in "OC"), immagino sappiate già di cosa si tratti, ad ogni modo riprendo dal manuale, considerando anche le precisazioni comunicate nel messaggio del Notiziario del 2 agosto 2010.
Nel caso in cui incontri una squadra piazzata peggio di te e la tua fiducia è forte o maggiore, i tuoi giocatori possono sottovalutare gli avversari e giocare al di sotto delle loro normali possibilità.
Il rischio di sottovalutare l'avversario dipende dalla differenza di punti e di posizione tra le due squadre, dal tuo livello di fiducia e dall'atteggiamento della tua squadra per la partita. Più grande è la differenza tra le squadre, più alta è la fiducia, maggiore è il rischio. Il solo modo per evitare completamente il rischio di sottovalutare l'avversario è quello di giocare "partita della stagione".
Nel caso in cui la tua squadra sottovaluti l'avversario, i punti di differenza, il livello della fiducia, l'atteggiamento della squadra e il fattore campo, sono i fattori che ne determinano l'entità. In base al risultato puoi però recuperare nell'intervallo tra i due tempi: recupero totale se in svantaggio, 2/3 se in pareggio, 1/3 se in vantaggio di un gol.
Notate che la sottovalutazione può accadere solo nelle partite di campionato, ma non nelle prime tre giornate.
Allora sembra piuttosto chiaro: la probabilità che vi sia OC è legata a 4 variabili:
- La Differenza di Posizione
- La Differenza di Punti
- Il Livello della Fiducia
- L'Atteggiamento (Mots, Normal, Pic)
mentre l'intensità dell'OC è legata a 4 variabili:
- La Differenza di Punti
- Il Livello della Fiducia
- L'Atteggiamento (Mots, Norma, Pic)
- Il fattore campo
a differenza delle 4 sopra manca la Differenza di Posizione e si aggiunge il fattore campo.
La ricerca DAC
In DAC è stato raccolto un campione di 90 partite. In 3 partite l'atteggiamento è stato "Partita della stagione" (Mots) e non c'è stata OC, come da manuale. Il campione effettivo quindi è di 87 partite. Vediamo come varia la presenza o meno di OC al variare delle 4 variabili:
1) La Differenza di Posizione
Questo valore può varia da 2 ad un massimo di 7 (nel caso in cui un team sia primo e l'altro ottavo), questi i dati:
La ricerca DAC
In DAC è stato raccolto un campione di 90 partite. In 3 partite l'atteggiamento è stato "Partita della stagione" (Mots) e non c'è stata OC, come da manuale. Il campione effettivo quindi è di 87 partite. Vediamo come varia la presenza o meno di OC al variare delle 4 variabili:
1) La Differenza di Posizione
Questo valore può varia da 2 ad un massimo di 7 (nel caso in cui un team sia primo e l'altro ottavo), questi i dati:

vedete nella prima riga che nel caso di differenza di posizioni pari a 2 abbiamo 8 casi in cui non c'è OC e nessun caso di OC. Con una differenza di posizioni pari a 3 ci sono 5 casi senza OC e 2 casi di OC, 2 casi su 7 sono il 28.57%. E così via a crescere. Vedete che a valori di differenza di posizioni pari a 5, 6 o 7 l'OC sembra assestarsi attorno a valori sul 45/50%.
Se rappresentiamo in un grafico vediamo come la probabilità di OC cresca al crescere delle differenze di posizione.
Se rappresentiamo in un grafico vediamo come la probabilità di OC cresca al crescere delle differenze di posizione.

2) La Differenza di Punti
Nel campione questo valore varia da 0 a 30.
Nel campione questo valore varia da 0 a 30.
 Come ci aspettavamo la probabilità di OC cresce al crescere della differenza punti, fino a diventare quasi una certezza per differenze superiori ai 20 punti.
Come ci aspettavamo la probabilità di OC cresce al crescere della differenza punti, fino a diventare quasi una certezza per differenze superiori ai 20 punti. Gli ondeggiamenti della curva sono normali in un campione così ristretto, ma la linea di tendenza parla chiaro.
Gli ondeggiamenti della curva sono normali in un campione così ristretto, ma la linea di tendenza parla chiaro.3) Il Livello della Fiducia
La fiducia può assumere i valori di 5 ("forte"), 6 ("magnifica"), 7 ("leggermente esagerata") e 8 ("esagerata").

per valori pari a 5 non c'è nessun OC, con fiducia pari a 6 il 28% dei casi, con fiducia pari a 7 circa il 47%, con fiducia pari a 8 poco meno del 40% (ma il dato può essere inficiato dai pochi dati disponibili con fiducia pari a 8).
Questo il grafico della probabilità di OC al variare del livello di Fiducia:
Questo il grafico della probabilità di OC al variare del livello di Fiducia:

4) L'Atteggiamento (Mots, Normal, Pic)
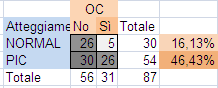
Si passa dai 5 soli casi giocando normal (il 16%), al 46% dei casi giocando Pic.

Alla ricerca di una FORMULA
Ora quanto visto sopra ci dà un idea di massima di come vari la fiducia al variare delle singole variabili. Per stimare però quanto pesi una variabile rispetto all'altra occorre considerarle tutte insieme e fare un'analisi di regressione.
In sostanza si tratta di stimare i valori a, b, c, d ed e della seguente
cercando di ottenere una formula della probabilità di OC, formula da prendere con le pinze data la ristrettezza del campione.
Anche l'uso del termine Probabilità è un po' improprio dato che il valore finale non sarà compreso tra 0 e 1, ma potrà anche valere un po' di più o di meno.
Vi salto i tecnicismi e salto alla conclusione dicendo che una stima di questo tipo non dava risultati attendibili. Allora ho provato a pensarci un po' e mi sono accorto che le variabili "Differenza di posizione" e "Differenza punti" non sono mutualmente indipendenti, ma sono correlate (maggiore la differenza punti, maggiore sarà la differenza di posizione dei due team in linea di massima), se non sono completamente arrugginito di queste cose un'analisi di regressione efficace richiede la mutua indipendenza delle variabili.
Ho provato ad escludere la "Differenza Punti", ma l'efficacia della stima (l'R-quadro per gli statistici) crollava, mentre togliendo la "Differenza di Posizione" si otteneva una formula decente.
Del resto la "Differenza di Posizione" non fa neppure parte delle 4 variabili che regolano l'intensità dell'OC (vedi sopra la citazione dal manuale), per cui escluderla dal calcolo della probabilità dell'OC non sembra un sacrificio insensato (tenendo anche conto come detto che parte dell'informazione è comunque implicita nella differenza punti).
Ponendo l'Atteggiamento pari a "1" se si gioca Normal e a "2" se si gioca Pic, la formula della probabilità di OC sembra poter essere:
In sostanza si tratta di stimare i valori a, b, c, d ed e della seguente
Probabilità di OC = a*Diff.Posiz. + b*Diff.Punti + c*Fiducia + d*Atteggiamento + e
cercando di ottenere una formula della probabilità di OC, formula da prendere con le pinze data la ristrettezza del campione.
Anche l'uso del termine Probabilità è un po' improprio dato che il valore finale non sarà compreso tra 0 e 1, ma potrà anche valere un po' di più o di meno.
Vi salto i tecnicismi e salto alla conclusione dicendo che una stima di questo tipo non dava risultati attendibili. Allora ho provato a pensarci un po' e mi sono accorto che le variabili "Differenza di posizione" e "Differenza punti" non sono mutualmente indipendenti, ma sono correlate (maggiore la differenza punti, maggiore sarà la differenza di posizione dei due team in linea di massima), se non sono completamente arrugginito di queste cose un'analisi di regressione efficace richiede la mutua indipendenza delle variabili.
Ho provato ad escludere la "Differenza Punti", ma l'efficacia della stima (l'R-quadro per gli statistici) crollava, mentre togliendo la "Differenza di Posizione" si otteneva una formula decente.
Del resto la "Differenza di Posizione" non fa neppure parte delle 4 variabili che regolano l'intensità dell'OC (vedi sopra la citazione dal manuale), per cui escluderla dal calcolo della probabilità dell'OC non sembra un sacrificio insensato (tenendo anche conto come detto che parte dell'informazione è comunque implicita nella differenza punti).
Ponendo l'Atteggiamento pari a "1" se si gioca Normal e a "2" se si gioca Pic, la formula della probabilità di OC sembra poter essere:
Probabilità di OC = 0.04*Diff.Punti + 0,08*Fiducia + 0,16*Atteggiamento - 1
sembra anche facile da ricordare, i decimali infatti sono 4 per la Differenza Punti, 8 per la fiducia e 16 per l'Atteggiamento.
Come funziona questa formula sul campione? Presto detto
se è minore del 50% non c'è OC in 49 casi e c'è OC in 7 casi (di cui due appena sopra al limite, al 52%)
se è maggiore del 50% non c'è OC in 8 casi (di cui tre appena sotto al limite, al 48%) e sì OC in 23 casi
se la formula è maggiore del 70% non ho OC solo in 1 caso su 14 (pari al 7%)
se la formula è minore del 30% c'è OC solo in 3 casi su 41 (ancora pari al 7%)
Ecco in un grafico le 7 partite particolarmente fortunate in cui non c'è stata OC, pur con un valore della formula superiore al 50%, nel resto del campione non c'è stata OC, come previsto dal valore basso dato dalla formula.
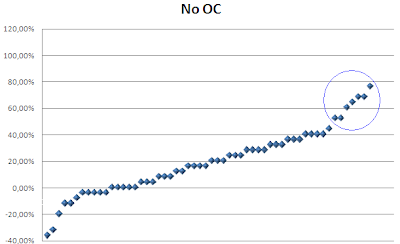
Passando infine ai valori di Probabilità di OC calcolata per quelle partite nel campione che invece hanno avuto OC

vedete che sono solo 4 i casi sfortunati di OC prevista inferiore al 40% e invece realizzatasi. 4 i valori compresi tra 40% e 50% (di cui 3 al 48%) e altri 23 con probabilità superiore al 50% in cui poi l'OC si è concretizzata.
Le Cause dell'OC
Il fatto che i decimali per la differenza di punti siano 4, quelli per la fiducia 8 e quelli per l'atteggiamento 16 non significa che queste variabili siano nel medesimo ordine di importanza, dato che variano su scale diverse (da 0 a 30 la differenza punti, da 5 a 8 la fiducia e da 1 a 2 l'atteggiamento). Portando tutto sulla stessa scala e cioè sostituendo ai valori di fiducia il valore (Fiducia-5)*10 e all'Atteggiamento 0 se Normal e 30 se Pic, la formula diventa:
Insomma la Differenza Punti sembra pesare oltre 5 volte il valore della Fiducia e 8 volte il valore dell'Atteggiamento.
Quindi - e questo è importante - se troviamo OC in squadre che hanno piccato, non è tanto il Pic in sé a essere causa di Overconfidence, ma il fatto che il Pic viene fatto da squadre che hanno tanto vantaggio di punti sull'avversario.
Complessivamente l'OC dipende quindi per oltre il 75% dalla differenza punti, per il 14% dal livello di fiducia e per il 10% dall'Atteggiamento.
La metto in un grafico a Torta che forse resta più impressa:
Probabilità di OC = 0.04*Diff.Punti + 0,0075*Fiducia(riscalata) + 0,005*Atteggiamento(riscalato) - 0.45
Insomma la Differenza Punti sembra pesare oltre 5 volte il valore della Fiducia e 8 volte il valore dell'Atteggiamento.
Quindi - e questo è importante - se troviamo OC in squadre che hanno piccato, non è tanto il Pic in sé a essere causa di Overconfidence, ma il fatto che il Pic viene fatto da squadre che hanno tanto vantaggio di punti sull'avversario.
Complessivamente l'OC dipende quindi per oltre il 75% dalla differenza punti, per il 14% dal livello di fiducia e per il 10% dall'Atteggiamento.
La metto in un grafico a Torta che forse resta più impressa:

APPENDICE
Questo il campione nel dettaglio:



PS. dai un occhio all' INDICE del blog, ci sono parecchi articoli che ti potrebbero interessare.
Andreac (team ID 1730726 in Hattrick)
Andreac (team ID 1730726 in Hattrick)

This opera by Andreac is licensed under a Creative Commons Attribuzione-Non commerciale 3.0 Unported License. Cioé questo lavoro può essere liberamente copiato, distribuito o modificato senza espressa autorizzazione dell'autore, a patto che l'autore sia chiaramente indicato e la pubblicazione non sia a fini commerciali.


5 commenti:
Articolo ottimo come sempre, però sinceramente mi sembra che il campione sia davvero troppo piccolo per un'analisi quantitativa,
inoltre escludere la differenza di posizione (la cui correlazione lineare mostrata nel grafico mi sembra abbastanza pronunciata) mi sembra un po' "forte" come ipotesi...
ciao Luca
allora, riguardo alla ristrettezza del campione siamo tutti d'accordo... all'inizio ero anch'io un po' restio a fare qualche analisi quantitativa, però guardando i dati mi sono reso conto che dovevo pur esprimere il fatto che ci sono ben 30 casi di "non OC" pur in presenza di PIC... e di situazione piuttosto simile anche per la Fiducia... un'analisi che tenesse conto di tutte e tre le variabili era necessaria per esprimere il peso di una variabile rispetto alle altre
Riguardo l'esclusione della differenza di posizione, qui non ho approfondito per non entrare in eccessivi tecnicismi, il fatto è che - PRIMA di accorgermi che il calcolo dell'Intensità dell'OC non ne tiene conto - mi ero reso conto che qualcosa non tornava. Se consideravo le 4 variabili assieme mi veniva un valore negativo per il coefficiente della diff. di posizione, che stava a indicare una correlazione con inversa proporzionalità. Tale correlazione era naturalmente in contrasto con la prima analisi, quella a "variabili separate"... Il ragionamento sul fatto che l'informazione contenuta nella differenza di posizione è in gran parte contenuto nella diff. di punti mi ha portato a escluderla dall'analisi e i valori ottenuti erano molto migliori. Il campione ristretto non mi consente di poterlo dire con certezza, ma personalmente sono piuttosto convinto che la diff. di posizione non influisca per nulla sulla probabilità di OC (cosa che qui mi sono limitato a presentare come ipotesi di lavoro) tanto quanto nulla incinde nell'intensità dell'OC stessa.
A
Hai preso in considerazione il fatto che il contributo della differenza di posizione possa non essere lineare?
Per esempio la posizione potrebbe essere usata semplicemente come test iniziale on/off (due o meno, off, non si guarda niente del resto, semplicemente non c'e' OC, tre o piu' on, puo' esserci OC).
Ciao.Fabio.
P.S.: gran bel lavoro, adesso andrebbe verificata la formula ricavata da quel campione su nuove istanze esterne al campione per vedere se mantiene all'incirca la stessa percentuale di successi.
Potrebbe.
Non so però dire di quanto possa spostare le conclusioni.
Natualmente se qualcuno facesse un'altra ricerca sarebbe interessante confrontare i dati.
Studio bellissimo.
Solo: non è che sarebbe possibile integrare nelle tabelle dei campioni anche il delta-posizione, anche se tu non lo usi nella forumala?
Cia.Fabio.
Posta un commento