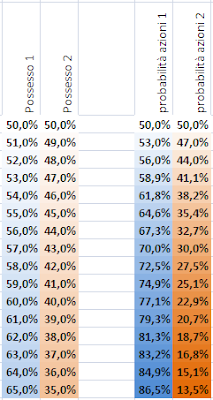
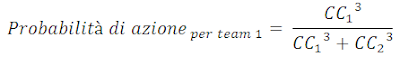AVVERTENZA: I Valori Esposti in questo articolo sono obsoleti, nuovi valori sono esposti nell'articolo HATTRICK - Risultati Finali del Feedback e Prediction F
2 Il quantitativo di perdita non è uguale per tutti i settori
La perdita per i centrocampisti centrali è circa il doppio di quella dei difensori.
Quindi
Xm=2*Xd
Ym=2*Yd
Per gli attaccanti si assesta circa alla metà dei due casi precedenti.
Xa=1.5*Xd
Ya=1.5*Yd
inoltre
i difensori centrali e gli attaccanti riceveranno un bonus (ma non i centrocampisti centrali). Questo bonus equivale alla perdita di contributo che ricevono due giocatori, cioè usare due attaccanti o due difensori sarà lo stesso rispetto al passato
viene introdotto un "bonus compensativo" per difensori e attaccanti in TUTTE le skill, pari a
1/(1-Xd) per i difensori e
1/(1-Xa) per gli attaccanti, cioé, sapendo la relazione che li lega, 1/(1-1.5*Xd)
se Xd=5% allora
per i difensori il bonus sarà del 5.26%
per gli attaccanti del 8.10%
NOTA: visto che ricevo diverse osservazioni su questo punto vorrei chiarire ancora. I bonus vanno a TUTTI i difensori, poi se gioca in 1 nessun malus, in due malus X e in tre malus Y. I malus si applicano DOPO. Quindi se moltiplichiamo DOPO per (1-Xd) l'unico modo di annullare tale modifica è quello di moltiplicare PRIMA per 1/(1-Xd)
dovendo applicare un malus del 10% ad es.
se prima diamo un bonus del 10% e poi un malus del 10%
100 + 10% = 110
110 - 10% = 99 e non siamo a 100
quindi dobbiamo fare 100 + 1/(1-0.10) cioè aggiungere l'11.1111111% per poi poter togliere il 10% e tornare ad avere 100
3 Promuovere rose più ampie e bilanciate
Qui avevo seguito la traduzione inglese "if you use two high level midfielders the third one will have to be at a level even teams in div X wouldn’t field that often to penalise you – so scenarios like that are rare" e "high level" è decisamente indefinito poi ho visto la traduzione in italiano "se usi due centrocampisti titanici il terzo dovrà essere di un livello che nemmeno le squadre di X serie mettono in campo così spesso" questa versione è più precisa e corretta, anche in svedese "om man har två titaniska mittfältare" e in molte altre lingue si indica chiaramente "15".
Questo è un punto di non poca importanza perché è l'unico appiglio che abbiamo per stimare Y.
Dalle formule che ho mostrato in altri articoli, ipotizzando giocatori monoskill con 6 di forma, 4 di resistenza, 4 di esperienza con 15 in primaria e 4 nelle secondarie ottengo un contributo di due centrocampisti (come descritto nell'editoriale) pari a 11.22.
Se li devo confrontare con centrocampo a 2 significa valutare quando sono pari a (1-X)*11.22
E quindi nel caso di terzo giocatore insufficiente
(1-X)*11.22=(1-Y)*12.82(1-Y)=(1-X)*0.875
Y=1-(1-X)*0.875
Y=0.875*X+0.125
Nel caso di terzo giocatore accettabile vale (saltando i passaggi)
Y=0.849*X+0.151
questo determina il seguente grafico al variare di X (X è in basso, nelle ascisse, e varia tra 5% e 15%, mentre Y è nelle ordinate)
 al variare di X vedete in blu l'ipotesi con terzo giocatore insufficiente e in rosso col terzo accettabile.
al variare di X vedete in blu l'ipotesi con terzo giocatore insufficiente e in rosso col terzo accettabile.
Più interessante ancora è considerare la variazione Y/X cioè quant'è il malus a tre giocatori rispetto al malus a due giocatori

valori troppo elevati sono poco credibili e HT-Tjecken ha chiarito che Y>2X come potete vedere in [post=13880492.536]
questo esclude che X sia > dell 11% o del 13%, per tali valori infatti Y è < y =" 2,25" style="text-align: justify;">
e quindi per le relazioni viste sopra:
teniamo per ora buoni questi valori e andiamo avanti... di
4 Esperienza nella formazione
5 Confusione
non parlo, mi sembrano piuttosto chiare
6 Modifiche al contributo dei giocatori
Generale: - Difensori centrali e attaccanti ricevono un bonus. Questo bonus equivale alla perdita di contributo dovuta ai due giocatori centrali. Nota che questo non è vero per gli attaccanti difensivi (vedi sotto).
se Xd è 4% allora il "bonus compensativo" sarà del
1/(1-0.04) = 4.16 % per i difensori e
1/(1-0.06) = 6.38 % per gli attaccanti
Regia: - Ali, difensori centrali e attaccanti difensivi perderanno parte della regia...per mantenere l'attuale bilanciamento relativo tra centrocampisti centrali e altre posizioni che usano la skill regia, così da non rendere più importante schierare ali verso il centro o attaccanti difensivi una volta che rendiamo i centrocampisti centrali meno forti
quindi c'è un "malus regia di adeguamento" Z per ali, dc, attaccanti dif.
con Xm attorno al 8% avevo immaginato che "per mantenere l'attuale bilanciamento relativo" la perdita Z fosse nell'ordine del 8%. Invece un utente svizzero, pumuel (secondo nella sua serie A), che qui ringrazio, mi ha segnalato una frase di HT-Tjecken in cui veniva affermato che questa perdita fosse compresa tra X e Y... allora mi sono messo a fare due conti (chi non ha voglia di vedere numeri può saltare direttamente alla conclusione)
il contributo pre-modifica in regia di ogni centrocampista normal era di 0,46825
3 centrocampisti danno 1.40475
una riduzione del 18% lo porta a 1.1519
2 centrocampisti apportano 0.9365
una riduzione del 8% lo porta a 0.86158
la differenza è di 0.2903
ora l'apporto precedente in regia di un'ala TM era 0,30659
è evidente che se così fosse sarebbe di gran lunga preferibile l'ala TM al terzo centrocampista
per portare l'apporto al 0.2903 serve una riduzione del (0.2903-0,30659)/0,30659 = del 5.30%... ed eccoci quindi a
un valore inferiore sia ad X (8%) che a Y (20%) .
Quindi il valore di confine di Z può essere qualsiasi numero compreso tra 8% e 20%... Ho lasciato appositamente 14,5% nelle prediction C per vedere se, in caso di giocatori con ordini individuali verso il centro avessi dei casi di sottostima.
E sottostima, seppur leggera, si è vista. Pertanto abbasso Z, il malus regia per DCO, ALI tm e ATT difensivi dal 14,5% al 10%. Siamo comunque superiori al 5.3% per cui il 3° cc sarà preferibile all'ala TM, come da editoriale.
Passaggi: - Attaccanti difensivi tecnici faranno anch'essi minor uso della loro skill passaggi al centro, ma un uso maggiore ai lati. La perdità è comunque maggiore rispetto al guadagno.
- Attaccanti difensivi non tecnici diventeranno più simili ai tecnici. La sola differenza sarà che i tecnici otterranno di più dai loro passaggi sui lati.
quindi non solo non hanno il bonus, ma i tecnici vengono COMPLETAMENTE equiparati ai non tecnici nell'attacco centrale e hanno un plus in quello laterale.
Avevo ipotizzato inizialmente un bonus sui lati del 7.5%. Tale valore si è rivelato molto inferiore a quanto necessario. Per far tornare i conti devo
1) introdurre anche per loro il bonus di reparto di base, pari a (1/0,94)%
2) alzare il bonus in passaggi dal 7.5% al 30%. Si avete letto bene, 30% (sempre sui coefficienti! non sulle percentuali)
Faccio notare che questo alza il loro contributo in passaggi nei lati dal coefficiente 0.2204 al 0.3048, una differenza inferiore in valore assoluto alla perdita al centro che è dal 0.4706 al 0.3224. Quindi "la perdita è maggiore del guadagno", come da editoriale.
Cross: Ali, terzini e attaccanti (specialmente verso l'ala) faranno maggior uso della loro skill cross, con l'eccezione dei terzini verso il centro, che la utilizzeranno meno.
maggiore quanto? avevo ipotizzato - del tutto arbitrariamente - un 7.5% di bonus (10% per lo "specialmente") e un 5% di malus.
Per quanto riguarda gli attacchi laterali risultano leggermente sottostimate le ali normali, sovrastimate le offensive (abbasso il bonus in cross dal 7.5% al 2.5%) e fortemente sottostimate le TM a cui assegno un +15% sia in passaggi che in cross.
Difesa: - Ali offensive e difensive useranno di più la loro skill difesa. - Difensori centrali verso l'ala contribuiranno di più con la loro difesa sul lato - Terzini difensivi perderanno un po' della loro difesa verso il centro
anche qui ipotizzo un 7.5% nei bonus e un 5% nel malus.
I DCO sono sembrati leggermente sottostimati in difesa laterale, ho assegnato loro un bonus del 4% (a quelli verso l'ala era stato assegnato uno del 7.5%). Terzini offensivi e soprattutto difensivi sono risultati sovrastimati nell'apporto alle difese laterali. Introduco un malus del 2% per i primi e del 3% per i secondi. Quelli verso il centro risultano un po' sottostimati. Assegno un bonus del 2.5%.
Le Ali TM erano un po' sottostimate in difesa laterale: estendo anche a loro il bonus del +7.5% già dato a difensive e offensive.
Parate: - I portieri contribuiranno leggermente meno con la loro skill parate, incidendo su entrambi i lati e centro.
Il malus in Parate, posto al 5% è sembrato leggermente eccessivo, i contributi sembravano un po' sottostimati, il malus è stato ridotto al 2%
Procedo ora a riconsiderare le tabelle calcolate da Flattermann (www.flattermann.net) per vedere i cambiamenti.
Ecco i nuovi valori A MONTE dei malus da sovraffollamento X e Y

LEGENDA
LE RIGHE
GK goalkeeper, portiere
CD central defender
WB wing back, terzino
IM inner midfielder, centrocampista centrale
WI winger, ala
FW forward, attaccante
off offensivo
def difensivo
tw toward wing, verso l'ala
tm toward middle, verso il centro
LE COLONNE
MID REG apporto di regia al centrocampo
CD Par apporto di parate alla difesa centrale
CD Dif apporto di difesa alla difesa centrale
SD Par apporto di parate alla difesa laterale (Side defence)
SD Dif apporto di difesa alla difesa laterale (Side defence)
CA Pass apporto di passaggi all'attacco centrale
CA Att apporto di attacco all'attacco centrale
SA Pass apporto di passaggi all'attacco laterale (Side attack)
SA Cro apporto di cross all'attacco laterale (Side attack)
SA Att apporto di attacco all'attacco laterale (Side attack)
e queste le variazioni totali, in %, PRIMA dei malus di sovraffollamento) rispetto ai valori della stagione precedente (che trovate nel sito di Flattermann http://www.flattermann.net/)

DOPODICHE' dobbiamo applicare i malus di sovraffollamento
per 2 giocatori in una zona
Xd=4%
Xm=8%
Xa=6%
per 3 giocatori in una zona
Yd=9%
Ym=18%
Ya=13.5%
TERZA VERSIONE del 21 MAGGIO
migliorata grazie ai risultati del Feedback ricevuto
Doverosa PREMESSA
Allora, come molti di voi, mi sono trovato un po' perplesso davanti all'editoriale dello scorso 19 marzo... per cercare di riordinare le idee ho cominciato a buttar giù un po' di numeri per capire i punti fermi del discorso di HT-Tjecken e cercare di interpretare le sue parole, aiutandomi anche grazie a Sam-Vimes-NH, frequentatore assiduo del forum Global, che ha raccolto in un thread alcune risposte di HT-Tjecken agli utenti che aprivano qualche spiraglio di luce sulla questione.
E' chiaro: sto cercando di tirare fuori numeri da parole, con tutte le incertezze del caso. Sono parole di un HT, ma sempre parole sono.
Alcune cose di quanto segue sono certe (i rapporti tra i malus di difesa e quello di centrocampo ad esempio), altre sono probabili, altre solo possibili (o intuibili, il rapporto Y/X che vedrete sotto ad esempio), altre sono completamente messe per intuizione (il bonus al trequartista nei passaggi laterali ad esempio). Quindi ci sono diversi gradi di certezza in quanto segue, vogliatene tener conto.
Qualsiasi stima sugli effetti tattici dell'editoriale (ad es se un tale modulo sarà più conveniente rispetto ad un altro ecc) abbisogna di un consistente numero di partite effettivamente giocate per potere fare stime fondate sull'ENTITA' di bonus e malus. Cercare di indovinare adesso mi sembra un azzardo assai poco fondato.
Come molti di voi sanno, abbiamo realizzato un sito per lo studio della questione dove troverete gli strumenti e informazioni http://sites.google.com/site/andreacprediction/
Procedo seguendo la logica dell'editoriale, le citazioni dall'editoriale sono in blu.
1 Contributo dei giocatori centrali
Quando un giocatore gioca da solo in posizione centrale contribuirà al 100%.
Quando due giocatori giocano in posizione centrale, entrambi perderanno un po' del loro contributo.
Quando tre giocatori giocano in posizione centrale, tutti loro perderanno ancor più del loro contributo.
Allora viene introdotto un "malus di sovraffollamento" in % (come spiegato dallo stesso HT-Tjecken)
migliorata grazie ai risultati del Feedback ricevuto
Doverosa PREMESSA
Allora, come molti di voi, mi sono trovato un po' perplesso davanti all'editoriale dello scorso 19 marzo... per cercare di riordinare le idee ho cominciato a buttar giù un po' di numeri per capire i punti fermi del discorso di HT-Tjecken e cercare di interpretare le sue parole, aiutandomi anche grazie a Sam-Vimes-NH, frequentatore assiduo del forum Global, che ha raccolto in un thread alcune risposte di HT-Tjecken agli utenti che aprivano qualche spiraglio di luce sulla questione.
E' chiaro: sto cercando di tirare fuori numeri da parole, con tutte le incertezze del caso. Sono parole di un HT, ma sempre parole sono.
Alcune cose di quanto segue sono certe (i rapporti tra i malus di difesa e quello di centrocampo ad esempio), altre sono probabili, altre solo possibili (o intuibili, il rapporto Y/X che vedrete sotto ad esempio), altre sono completamente messe per intuizione (il bonus al trequartista nei passaggi laterali ad esempio). Quindi ci sono diversi gradi di certezza in quanto segue, vogliatene tener conto.
Qualsiasi stima sugli effetti tattici dell'editoriale (ad es se un tale modulo sarà più conveniente rispetto ad un altro ecc) abbisogna di un consistente numero di partite effettivamente giocate per potere fare stime fondate sull'ENTITA' di bonus e malus. Cercare di indovinare adesso mi sembra un azzardo assai poco fondato.
Come molti di voi sanno, abbiamo realizzato un sito per lo studio della questione dove troverete gli strumenti e informazioni http://sites.google.com/site/andreacprediction/
Procedo seguendo la logica dell'editoriale, le citazioni dall'editoriale sono in blu.
1 Contributo dei giocatori centrali
Quando un giocatore gioca da solo in posizione centrale contribuirà al 100%.
Quando due giocatori giocano in posizione centrale, entrambi perderanno un po' del loro contributo.
Quando tre giocatori giocano in posizione centrale, tutti loro perderanno ancor più del loro contributo.
Allora viene introdotto un "malus di sovraffollamento" in % (come spiegato dallo stesso HT-Tjecken)
- 1 giocatore --> nessun malus
- 2 giocatori --> malus X
- 3 giocatori --> malus Y
2 Il quantitativo di perdita non è uguale per tutti i settori
La perdita per i centrocampisti centrali è circa il doppio di quella dei difensori.
Quindi
Xm=2*Xd
Ym=2*Yd
Per gli attaccanti si assesta circa alla metà dei due casi precedenti.
Xa=1.5*Xd
Ya=1.5*Yd
inoltre
i difensori centrali e gli attaccanti riceveranno un bonus (ma non i centrocampisti centrali). Questo bonus equivale alla perdita di contributo che ricevono due giocatori, cioè usare due attaccanti o due difensori sarà lo stesso rispetto al passato
viene introdotto un "bonus compensativo" per difensori e attaccanti in TUTTE le skill, pari a
1/(1-Xd) per i difensori e
1/(1-Xa) per gli attaccanti, cioé, sapendo la relazione che li lega, 1/(1-1.5*Xd)
se Xd=5% allora
per i difensori il bonus sarà del 5.26%
per gli attaccanti del 8.10%
NOTA: visto che ricevo diverse osservazioni su questo punto vorrei chiarire ancora. I bonus vanno a TUTTI i difensori, poi se gioca in 1 nessun malus, in due malus X e in tre malus Y. I malus si applicano DOPO. Quindi se moltiplichiamo DOPO per (1-Xd) l'unico modo di annullare tale modifica è quello di moltiplicare PRIMA per 1/(1-Xd)
dovendo applicare un malus del 10% ad es.
se prima diamo un bonus del 10% e poi un malus del 10%
100 + 10% = 110
110 - 10% = 99 e non siamo a 100
quindi dobbiamo fare 100 + 1/(1-0.10) cioè aggiungere l'11.1111111% per poi poter togliere il 10% e tornare ad avere 100
3 Promuovere rose più ampie e bilanciate
Qui avevo seguito la traduzione inglese "if you use two high level midfielders the third one will have to be at a level even teams in div X wouldn’t field that often to penalise you – so scenarios like that are rare" e "high level" è decisamente indefinito poi ho visto la traduzione in italiano "se usi due centrocampisti titanici il terzo dovrà essere di un livello che nemmeno le squadre di X serie mettono in campo così spesso" questa versione è più precisa e corretta, anche in svedese "om man har två titaniska mittfältare" e in molte altre lingue si indica chiaramente "15".
Questo è un punto di non poca importanza perché è l'unico appiglio che abbiamo per stimare Y.
Dalle formule che ho mostrato in altri articoli, ipotizzando giocatori monoskill con 6 di forma, 4 di resistenza, 4 di esperienza con 15 in primaria e 4 nelle secondarie ottengo un contributo di due centrocampisti (come descritto nell'editoriale) pari a 11.22.
Ora l'apporto di un giocatore molto più debole che ipotizzo tra 5 e 6 in primaria (dal forum: "what do you call a league 10 Inner? inadequate/passable?" "Somewhere around those lines, yes" HT-Tjecken, post 13865282.30) è tra 1.60 e 2.00
Ora dobbiamo valutare se il nuovo centrocampo è superiore o meno al precedente.
Il nuovo sarà (1-Y)*11.22+(1-Y)*1.6 oppure (1-Y)*11.22+(1-Y)*2, raccogliendo, (1-Y)*12.82 e (1-Y)*13.22
Ora dobbiamo valutare se il nuovo centrocampo è superiore o meno al precedente.
Il nuovo sarà (1-Y)*11.22+(1-Y)*1.6 oppure (1-Y)*11.22+(1-Y)*2, raccogliendo, (1-Y)*12.82 e (1-Y)*13.22
Se li devo confrontare con centrocampo a 2 significa valutare quando sono pari a (1-X)*11.22
E quindi nel caso di terzo giocatore insufficiente
(1-X)*11.22=(1-Y)*12.82(1-Y)=(1-X)*0.875
Y=1-(1-X)*0.875
Y=0.875*X+0.125
Nel caso di terzo giocatore accettabile vale (saltando i passaggi)
Y=0.849*X+0.151
questo determina il seguente grafico al variare di X (X è in basso, nelle ascisse, e varia tra 5% e 15%, mentre Y è nelle ordinate)
 al variare di X vedete in blu l'ipotesi con terzo giocatore insufficiente e in rosso col terzo accettabile.
al variare di X vedete in blu l'ipotesi con terzo giocatore insufficiente e in rosso col terzo accettabile.Più interessante ancora è considerare la variazione Y/X cioè quant'è il malus a tre giocatori rispetto al malus a due giocatori

valori troppo elevati sono poco credibili e HT-Tjecken ha chiarito che Y>2X come potete vedere in [post=13880492.536]
questo esclude che X sia > dell 11% o del 13%, per tali valori infatti Y è < y =" 2,25" style="text-align: justify;">
- Xm MALUS per 2 centrocampisti pari a 8%
- Ym MALUS per 3 centrocampisti pari a 18%
e quindi per le relazioni viste sopra:
- Xd=4% MALUS per i 2 difensori
- Yd=9% MALUS per i 3 difensori
- Xa=6% MALUS per i 2 attaccanti
- Ya=13.5% MALUS per i 3 attaccanti
teniamo per ora buoni questi valori e andiamo avanti... di
4 Esperienza nella formazione
5 Confusione
non parlo, mi sembrano piuttosto chiare
6 Modifiche al contributo dei giocatori
Generale: - Difensori centrali e attaccanti ricevono un bonus. Questo bonus equivale alla perdita di contributo dovuta ai due giocatori centrali. Nota che questo non è vero per gli attaccanti difensivi (vedi sotto).
se Xd è 4% allora il "bonus compensativo" sarà del
1/(1-0.04) = 4.16 % per i difensori e
1/(1-0.06) = 6.38 % per gli attaccanti
Regia: - Ali, difensori centrali e attaccanti difensivi perderanno parte della regia...per mantenere l'attuale bilanciamento relativo tra centrocampisti centrali e altre posizioni che usano la skill regia, così da non rendere più importante schierare ali verso il centro o attaccanti difensivi una volta che rendiamo i centrocampisti centrali meno forti
quindi c'è un "malus regia di adeguamento" Z per ali, dc, attaccanti dif.
con Xm attorno al 8% avevo immaginato che "per mantenere l'attuale bilanciamento relativo" la perdita Z fosse nell'ordine del 8%. Invece un utente svizzero, pumuel (secondo nella sua serie A), che qui ringrazio, mi ha segnalato una frase di HT-Tjecken in cui veniva affermato che questa perdita fosse compresa tra X e Y... allora mi sono messo a fare due conti (chi non ha voglia di vedere numeri può saltare direttamente alla conclusione)
il contributo pre-modifica in regia di ogni centrocampista normal era di 0,46825
3 centrocampisti danno 1.40475
una riduzione del 18% lo porta a 1.1519
2 centrocampisti apportano 0.9365
una riduzione del 8% lo porta a 0.86158
la differenza è di 0.2903
ora l'apporto precedente in regia di un'ala TM era 0,30659
è evidente che se così fosse sarebbe di gran lunga preferibile l'ala TM al terzo centrocampista
per portare l'apporto al 0.2903 serve una riduzione del (0.2903-0,30659)/0,30659 = del 5.30%... ed eccoci quindi a
un valore inferiore sia ad X (8%) che a Y (20%) .
Quindi il valore di confine di Z può essere qualsiasi numero compreso tra 8% e 20%... Ho lasciato appositamente 14,5% nelle prediction C per vedere se, in caso di giocatori con ordini individuali verso il centro avessi dei casi di sottostima.
E sottostima, seppur leggera, si è vista. Pertanto abbasso Z, il malus regia per DCO, ALI tm e ATT difensivi dal 14,5% al 10%. Siamo comunque superiori al 5.3% per cui il 3° cc sarà preferibile all'ala TM, come da editoriale.
Passaggi: - Attaccanti difensivi tecnici faranno anch'essi minor uso della loro skill passaggi al centro, ma un uso maggiore ai lati. La perdità è comunque maggiore rispetto al guadagno.
- Attaccanti difensivi non tecnici diventeranno più simili ai tecnici. La sola differenza sarà che i tecnici otterranno di più dai loro passaggi sui lati.
quindi non solo non hanno il bonus, ma i tecnici vengono COMPLETAMENTE equiparati ai non tecnici nell'attacco centrale e hanno un plus in quello laterale.
Avevo ipotizzato inizialmente un bonus sui lati del 7.5%. Tale valore si è rivelato molto inferiore a quanto necessario. Per far tornare i conti devo
1) introdurre anche per loro il bonus di reparto di base, pari a (1/0,94)%
2) alzare il bonus in passaggi dal 7.5% al 30%. Si avete letto bene, 30% (sempre sui coefficienti! non sulle percentuali)
Faccio notare che questo alza il loro contributo in passaggi nei lati dal coefficiente 0.2204 al 0.3048, una differenza inferiore in valore assoluto alla perdita al centro che è dal 0.4706 al 0.3224. Quindi "la perdita è maggiore del guadagno", come da editoriale.
Cross: Ali, terzini e attaccanti (specialmente verso l'ala) faranno maggior uso della loro skill cross, con l'eccezione dei terzini verso il centro, che la utilizzeranno meno.
maggiore quanto? avevo ipotizzato - del tutto arbitrariamente - un 7.5% di bonus (10% per lo "specialmente") e un 5% di malus.
Per quanto riguarda gli attacchi laterali risultano leggermente sottostimate le ali normali, sovrastimate le offensive (abbasso il bonus in cross dal 7.5% al 2.5%) e fortemente sottostimate le TM a cui assegno un +15% sia in passaggi che in cross.
Difesa: - Ali offensive e difensive useranno di più la loro skill difesa. - Difensori centrali verso l'ala contribuiranno di più con la loro difesa sul lato - Terzini difensivi perderanno un po' della loro difesa verso il centro
anche qui ipotizzo un 7.5% nei bonus e un 5% nel malus.
I DCO sono sembrati leggermente sottostimati in difesa laterale, ho assegnato loro un bonus del 4% (a quelli verso l'ala era stato assegnato uno del 7.5%). Terzini offensivi e soprattutto difensivi sono risultati sovrastimati nell'apporto alle difese laterali. Introduco un malus del 2% per i primi e del 3% per i secondi. Quelli verso il centro risultano un po' sottostimati. Assegno un bonus del 2.5%.
Le Ali TM erano un po' sottostimate in difesa laterale: estendo anche a loro il bonus del +7.5% già dato a difensive e offensive.
Parate: - I portieri contribuiranno leggermente meno con la loro skill parate, incidendo su entrambi i lati e centro.
Il malus in Parate, posto al 5% è sembrato leggermente eccessivo, i contributi sembravano un po' sottostimati, il malus è stato ridotto al 2%
Procedo ora a riconsiderare le tabelle calcolate da Flattermann (www.flattermann.net) per vedere i cambiamenti.
Ecco i nuovi valori A MONTE dei malus da sovraffollamento X e Y

LEGENDA
LE RIGHE
GK goalkeeper, portiere
CD central defender
WB wing back, terzino
IM inner midfielder, centrocampista centrale
WI winger, ala
FW forward, attaccante
off offensivo
def difensivo
tw toward wing, verso l'ala
tm toward middle, verso il centro
LE COLONNE
MID REG apporto di regia al centrocampo
CD Par apporto di parate alla difesa centrale
CD Dif apporto di difesa alla difesa centrale
SD Par apporto di parate alla difesa laterale (Side defence)
SD Dif apporto di difesa alla difesa laterale (Side defence)
CA Pass apporto di passaggi all'attacco centrale
CA Att apporto di attacco all'attacco centrale
SA Pass apporto di passaggi all'attacco laterale (Side attack)
SA Cro apporto di cross all'attacco laterale (Side attack)
SA Att apporto di attacco all'attacco laterale (Side attack)
e queste le variazioni totali, in %, PRIMA dei malus di sovraffollamento) rispetto ai valori della stagione precedente (che trovate nel sito di Flattermann http://www.flattermann.net/)

DOPODICHE' dobbiamo applicare i malus di sovraffollamento
per 2 giocatori in una zona
Xd=4%
Xm=8%
Xa=6%
per 3 giocatori in una zona
Yd=9%
Ym=18%
Ya=13.5%
PS. dai un occhio all' INDICE del blog, ci sono parecchi articoli che ti potrebbero interessare.
Andreac (team ID 1730726 in Hattrick)
Andreac (team ID 1730726 in Hattrick)
This opera by Andreac is licensed under a Creative Commons Attribuzione-Non commerciale 3.0 Unported License. Cioé questo lavoro può essere liberamente copiato, distribuito o modificato senza espressa autorizzazione dell'autore, a patto che l'autore sia chiaramente indicato e la pubblicazione non sia a fini commerciali.